NT,TN,NN,TT
不同厂商的规则不一样,我们现在是把以下情况称之为 NN,也就是 A 是行优先,B 是列优先的时候。 再具体点就是 A 和 B 都是 K 方向连续的时候,称之为 NN。
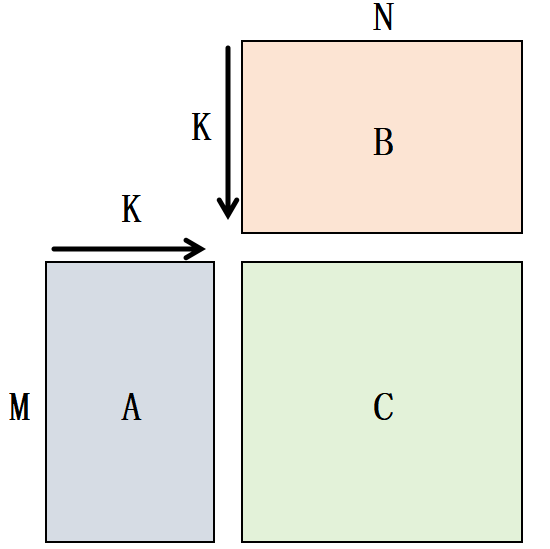
当 A 或者 B 的连续方向改变,就变成了 NT, TT, TN。用下表总结一下,我把最后一个维度作为连续的维度。 上图对应的就是 id=0 的记录。
| id | A | B | 注释 |
|---|---|---|---|
| 0 | [M, K] | [N, K] | NN |
| 1 | [M, K] | [K, N] | NT |
| 2 | [K, M] | [N, K] | TN |
| 3 | [K, M] | [K, N] | TT |
从数据加载的角度来看,A 和 B 都是 K 方向连续的时候性能是最好的,因为这时可以尽量合并使用 b128 的指令。 而且对于减少 L1 的 set 冲突也是很有效的。
GROUPED-GEMM
用 NN 的数据布局来举例,A 的形状是 [M, K], B 的形状是 [NUM_GROUPS, N, K],结果 C 的形状是 [M, N]。伴随 A 的有一个输入是 m_indicies,它是一个长度为 M 的一维数组,用来指定 A 的每一行使用 B 的哪一个 group 的权重来进行矩阵乘。
一般用于将多个小矩阵的乘拼接成一个大矩阵的乘,来增大对于硬件资源的利用率以及减小多个内核启动的开销。

BATCHED-GEMM
跟 groupd-gemm 类似,只不过每组的行数都是一样的,并且 C 不拼接到一起。也就是 [Batch, M, K] @ [Batch, N, K] -> [Batch, M, N],批处理矩阵乘。
GROUPED-GEMM-MASKED
跟 batched-gemm 类似,但是每个 batch 的有效的行数(M)可以不一样,通过一个额外的参数 masked_m 来指定每个 batch 的有效的行数是多少。形状是 [Batch, M_max, K] -> [Batch, N, K] -> [Batch, M_max, N]。